Astronomische Längeneinheiten

Eingestellt am 28. Oktober 2010 um 21:04 Uhr » Fotos Forschung und Wissenschaft Kommentar

Da ich mich gerade mit Astronomie und Astrophysik beschäftigt habe, tauchte die Frage nach den Nicht-SI-Einheiten zur Länge auf: (Wie) kann man sich diese (bildlich) vorstellen? Einerseits kann man Astronomie am Himmel, andererseits sind die Dimensionen sehr viel extremer als auf der beschaulichen Erde. Selbst die Entfernung zum nächsten Stern Alpha Centauri ist mit 4,34 Lichtjahren so groß, dass wir Menschen so schnell keinen Fuß auf einen möglichen Planeten in seinem System setzen werden. Von den extremen Temperaturen (2,7 K/-270,5 °C kosmischer Hintergrund bis hin zu etlichen Millionen Kelvin/°C im Inneren von Sternen), Dichten (150 g/cm³ in der Sonne, teilweise nur 1 Atom/cm³ im interstellaren Gas) oder Drücken (insbesondere in Neutronensternen) soll an dieser Stelle keine Rede sein.

Das oben genannte Lichtjahr ist definiert als die Entfernung, die das Licht mit seiner Geschwindigkeit von 299792458 ms^-1 in einem julianischem Jahr, das sind 365,25 Tage, zurücklegt. Nach der Umrechnung des Jahres in Sekunden folgt daraus eine handliche (?) bzw. anschauliche (?) Entfernung von rund 9,461×10¹² km bzw. 9,461 Billionen Kilometer. Der Vorteil dieser Einheit ist allerdings die Abschätzung, wie lange das Licht von einem entfernten Objekt zum Beobachter unterwegs ist. Das Licht von Alpha Centauri ist zu uns also 4,34 Jahre unterwegs.

Aus der Entfernungsmessung stammt die Einheit Parsec, kurz für Parallaxen-Sekunde. Das Parsec (pc) ist definiert als die Entfernung, unter der man eine Astronomische Einheit, das ist die mittlere Entfernung zwischen Erde und Sonne, 149,598×10⁶ km, unter einer Bogensekunde (1/3600stel Grad) sieht. Zur Berechnung dieser Entfernung und zur Visualisierung der Bogensekunde soll folgende nicht-maßstäbliche Abbildung dienen (schnell erstellt mit dem genial einfachen Zeichenprogramm Tgif):

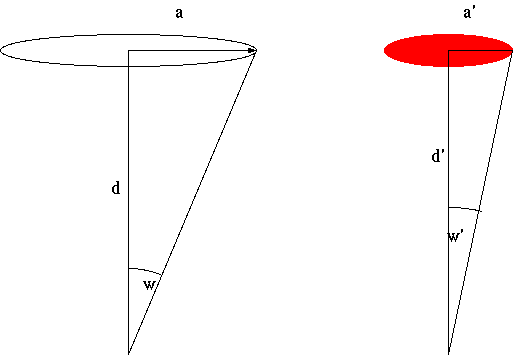
Damit die Entfernung d = 1 pc, muss bei a = 149,598×10⁹ m der Winkel w im Bogenmaß 2π/(360×3600) sein. In dem Dreieck gilt: tan(w) = a/d, umgestellt nach d =a/tan(w). Damit ist 1 Parsec rund 3,086×10¹³ km, also 30,86 Billionen Kilometer oder 3,26 Lichtjahre lang – ebenfalls eine handliche (?) Größe, aber immerhin anschaulich.

Nun noch kurz zur Frage nach der Bogensekunde: Unter dem Winkel w' = 1 Bogensekunde erscheint die in rechten Bild dargestellte 1-Cent-Münze, Radius a' = 8,125 mm in einer Entfernung d' = 1675,902 m, rund 1,7 Kilometern. Da muss man schon gute Augen haben.

Vielleicht erklärt dieser herausgearbeitete Unterschied zwischen beiden Einheiten und der Unterschied zu SI-Einheiten auch die Popularität des Lichtjahrs in der Literatur. Während höhere Potenzen des Meter (nach Kilo hätten wir ja noch Mega, Giga, Tera, … im Angebot) nur die Unvorstellbarkeit ausdrücken und das Parsec eine „physikalische“ Einheit ist, verbindet der Leser mit dem Lichtjahr vielleicht die Reise des Lichts oder eines Raumschiffs mit Lichtgeschwindigkeit (oder schneller, was es in der Fiktion geben soll).